Nick Timmons
Technical Software Research Engineer
Experience
Huawei Research UK, Principal Engineer
2021-2022
At Huawei, I work on automated low-level graphics benchmarking and research with new and emerging graphics technology.
Samsung R&D UK, Senior Android Graphics Developer
2021
At Samsung, I worked on proprietary graphics algorithms and Android graphics driver development. I was also involved in the benchmarking and evaluation of new Samsung devices.
Tencent, Robotics X, PhD Researcher
Summer 2019
In a break from my PhD, I took my experience with graphics, robotics and optimisation to Tencent where I:
Developed a fully operational telepresence device with the Robotics X team and led the development of multi-view merging augmented reality features to allow complex remote manipulation in extreme conditions.
Presented our robot at WAIC during a joint meeting between Elon Musk and Pony Ma.
Published our initial work on augmenting videos feeds to allow for useful vision around objects which obstruct the view of the manipulation arms. (Published in Human Robotics Interaction 2020: Augmented Reality with Multi-view Merging for Robot Teleoperation).
Took part in cultural exchange events where I developed my mandarin skills and won the a Tencent weight lifting competition.
Supervised junior interns in their projects and research. Including support with writing research papers and coding design.
As the only non-Chinese person in my team I developed my communication skills and understanding of Chinese-style engineering and business approaches.
AMD, Radeon Technologies Group, Senior Developer
April 2016 - January 2018
Working at AMD was a dream job for me. As part of the Radeon Technologies group I was able to work with some of the best and most prominent researchers and engineers in graphical computing and develop my own skills through supporting work with a diverse group of companies. Amongst many exciting projects at AMD, I was able to work on:
Development and optimisation for tasks of SSG cards - a first of its kind SSD on-board GPU. Working on this project I developed a technique to allow for 8k resolution, 60fps video editing in Adobe Premier Pro. A feature which is becoming more required each year as we move towards ever higher editing resolutions for film, music and television.
The work on the SSG development and optimisation was presented at Siggraph 2017 alongside many demos I fully developed or worked alongside other engineers to support.
These demos projects included:Early examples of GPU enabled AI for image denoising in real-time.
Novel approaches for global illumination using object aligned disk probes.
Ultra-high density mesh rendering through Host-GPU memory streaming.
Real-time raytracing using Radeon Pro Render for highly complex scenes. (This was a year and a half before NVidia’s RTX announcements).
Coordinated with CEO Lisa Su and then Senior Vice-President Raja Koduri to enable live demoing of our work at Siggraph on live machines without having to use pre-recorded demos. This involved ensuring demo stability and implementing last-minute changes to match with the speeches they had prepared.
Part of my role was in developer support. These requirements allowed me to:
Work with Unity Technologies to develop the real-time GPU lightmapper, a tool which is currently a key part of their light baking process in their widely used Unity game engine.
Presented a talk on optimised ray-tracing and lightmapping at Unity Technology’s yearly internal graphics development meet-up in Seattle.
Work with Adobe on Premiere Pro for the SSG integration, as well as bringing GPU acceleration to many products in the Creative Cloud suite, including Photoshop.
Work with Dassault Systèmes on Solidworks to optimise rendering times for VR and with Radeon Pro Render.
Work on Blender performance optimisation for AMD GPUs.
Work with many smaller companies to track and find solutions to problems specific to AMD GPU and drivers.
During my time at AMD was the official launch of the Vulkan graphics API. To allow fast learning and adoption of this new tool for rendering, I wrote internal documentation for Vulkan development and performance optimisation guides. I was able to quickly take on this project due to my previous experience in the Beta program for AMD’s Mantle API which was a major influence on the development and style of Vulkan.
One my favourite contributions when working with this team was in out reach and communication. As a more chatty member of the team I was often given the opportunity to work on the floor at events to present new research and technology developments. This experience allowed me to meet very interesting people and learn how best we could support them with new tools and technologies.
Siggraph 2017 presentation of SSG graphics, including demonstrations of my work and contributions:
AmBX, IoT Engineer
2015-2016
AMBX is an IoT start-up funded by Phillips. They specialise in large-scale lighting control systems with generic controller interfaces to allow for smart and adaptive lighting. During my time at AMBX I developed:
Novel control systems linked to PoE (power-over-ethernet) networks for remote accessibly and experience control.
3D simulation systems for pre-planned lighting control.
Development of the core technologies used for modelling circadian rhythm based lighting.
App development on iOS, Android and Desktop.
Improving the internal infrastructure to allow for maintainability and growth.
On-site installation and configuration of lighting and lighting control systems.
This results of this work are now in use in large scale spaces such as the famous AO Manchester Arena, but also in upscale bars and conference centres who use the control systems to improve the experience of its guests and provide unique environments which are not possible or so easily accessible with traditional configurations.
Frontier Developments, Graphics Developer
2012 - 2015
Working primarily on the development of the graphics systems in Elite: Dangerous but also supporting other games when needed.
The most prominent example of my work for this game are the development of the procedural planet systems, planetary ring systems, UI effects and lighting. Both systems allow for rendering at both the interplanetary scale and very close. Enabling this trick required complex approaches to give the impression of details which were not currently loaded and then matching them when the player approached. The game and systems we made make this one of the only games to allow traversal through a real imitation of the full milky way galaxy constructed with real data for known locations as well as using complex models to generate approximations for stars and systems which are not currently observable.
As a graphics developer I worked closely with the art team, providing my own art assets and developing pipelines for direct artistic control.
Included to the right is the PS4 release trailer, and a user created video from around the time I left the company, which features many graphical effects I was responsible for, or involved with the development of.
Outside of direct development, I also led the beginning of a partnership with AMD to provide test devices and support. Including early prototyping within Frontier of the Mantle graphics API (an early low-level GPU API which acted as a blueprint for Vulkan).
Double 11, Graphics Developer
2011-2012
First job in the games industry. I came in near the end of development on Little Big Planet Vita, and then began work on creating a system for porting and localising games from PC to the games consoles which were popular at the time. This involved the development of a large cross-platform library to link into existing projects as well as supporting tools for compiling specific games and their resources to the required formats.
This library and toolset was initially used for Frozen Synapse and Limbo, but was then later expanded for use on more ported games.
My time with Double 11 involved working in close communication with Sony engineers to learn the abilities and limitations of the Sony platforms, specifically to aide in development for the computationally limited Playstation Vita. It was in this job that I really began to become fascinated with optimisation and approximations to allow portability to weaker hardware without compromising on the experience or result in a meaningful way.
Due to the small size of the indie team, I was often recruited into other roles to fill gaps and ensure we could meet deadlines. This meant being closely involved with the art and design teams which in the long term has been a real benefit to me by giving me more skills and experience working around problems with limited resources.
Nicander, Placement Engineer
2010-2011
As part of my undergraduate degree I spent a year working with Nicander on their traffic control systems. At the time I joined the company work had just begun on expanding the Stockholm inner city traffic control system into one which would encompass the entirety of Sweden. Again working with a small team gave me the chance to experience many different areas of this very large and safety critical system.
In my time working on the project amongst other tasks, I was in charge of ensuring the safe transfer and upgrade from the then windows 98 based system to Windows 7, upgrading the map rendering system so that it could support displaying all information for every traffic light, bridge, tunnel system and associated networked devices for the entirety of Sweden, and general development of critical emergency reporting tools.
This allowed me to take advantage of my graphics background to provide modern implementations of rendering solutions to a project that would have otherwise struggled under the load of the sheer number of assets which needed to be controlled and accessed efficiently in an emergency. I also learned about real-scale database management and control from experts and had the opportunity to work with an `expert system’ for the first time.
During my time on the project we worked closely with the Swedish government and had to implement and maintain extensive testing and verification systems so that the system could be used without risk to the life or safety of road users.
While this job may appear to be the least glamourous of those on this list, working with a small team on critical nationwide infrastructure was very rewarding and allowed for branching out and learning new skills which hopefully helped keep people safe on roads which have some of the most dangerous weather conditions, and that is highly rewarding in itself.
Education
University of Cambridge, Cambridge, UK
PhD. APPROXIMATE COMPUTATION
Expected Graduation March 2021
PhD Overview:
My PhD focuses on solving the problem of safe approximation in mathematical computing programs. The work sought to find a standardised approach to perform code-level transforms to produce lower-accuracy implementations of human written functions without compromising the total error-tolerance of the function.
By identifying the “Three Step Approximation Problem” and investigating existing approximations which are currently in use, we were able to automatically generate new permutations of functions at different levels of error and prove that they were able to replace existing functions without a negative impact on the overall program.
The thesis demonstrates this finding by first considering current understandings of equality in software development, showing the current error in existing programs and how it can be exploited, and then demonstrating the use of the tools that were developed to solve this problem automatically on a number of case studies.
Publications:
Augmented Reality with Multi-view Merging for Robot Teleoperation - HRI 2020
An Empirical Analysis of IEEE-754 Elementary Function Libraries - Transactions on Mathematical Software (Pending)
Design-space exploration of LLVM pass-order with simulated annealing - EuroLLVM 2016
Approximating Activation Functions - self-published on arXiv
Additional Work:
Helped run the Friday evening “Happy Hour” in the fishbowl at the William Gates Building.
Long standing member of the University American Football team
Won awards for sporting positional performance.
Awarded Half-Blue status for competing at the highest level of American Football in the UK, and membership to the Hawks Club
Organised and did the technical setup for charity and sponsor events at the Computer Laboratory.
Consulting on new graphics developments for investing businesses.Development of libraries for the Julia programming language, including a correctly-rounded fast 32-bit mathematical functions, updates to support for GPU machine learning in Flux.ML and a number of image editing functions for the Images package.
Teaching:
Khalifa University, Abu Dhabi, UAE:
Teaching robotics and programming to gifted students from Abu Dhabi at the invitation of Sheikh Khalifa bin Zayed bin Sultan Al Nahyan
University of Cambridge, Cambridge, UK:
Supervising: Introduction to Graphics (3 years), Further Graphics (2 years), and Algorithms (3 years).
Teaching Assistant: Machine learning for programming
Additionally, I also updated the undergraduate graphics modules lecture material in 2018.
University of Cambridge, Cambridge, UK
MPhil. ADVANCED COMPUTER SCIENCE
Graduated May 2016
My masters course at Cambridge University was part taught and part research. I chose low-level programming, compiler design and machine learning modules. This involved analysing and validating network standards, implementing my own compiler optimisation system and design a machine learning based program for detecting early signs of diabetes in hospital patients.
My dissertation was on Multi-focal VR. In this work, I constructed a multi-focal VR desk based headset using multiple displays and then programmed a specific rendering engine for splitting images across different “focal planes” so that they can be merged into the users vision within the headset with approximated focal lengths. Once the system was ready and able to rendering complex scenes with focal depth information, I designed an experiment to be able to determine if the new focal cues gave any benefit to depth perception when compared to other depth cues.
The experiment involved intentionally reducing the effectiveness of different depth cues and then testing many users ability to differentiate the depth order of many objects on the screen.
The conclusion of this work was that focal depth is a strong depth indicator, but we also found some data which matched with current research in VR suggesting that a not insignificant proportion of the population is unable to discern depth from stereoscopic vision alone. For these users the focal depth cues were particularly effective and giving a real ability to perceive correct depth of objects.
Additional Work:
During this course I won multiple awards for University level sport.
Teesside University, Middlesbrough, UK
B.S. COMPUTER GRAPHICS SCIENCE
Graduated May 2012, First Class
During my time at Teesside University, I finished top of my class, worked on real-time ray tracing, optimised GPU based cloth simulation, and screen-space techniques for realistic subsurface scattering.
My final year project was on “Skin and Androgenic Hair Rendering” which won “Best in Show” at ExpoTees in 2012. This event is a showcase of local university tech projects.
I attended Teesside University at the advice of Pixar after discussing at Animex the potential for placement within that company during my second year of study. Unfortunately this was not able to be achieved due to visa issues, but this allowed me to work on more complex real-world systems and gain an understanding of the type of work I wanted to do. I would particularly like to praise Tyrone Davidson, Eudes Diemoz and Dr. Gordon Marshall for there extensive support in my study and of some of my more silly programming ideas, as well as giving very practical and useful lessons on how to be a good developer.
Additional Work:
During this course I played on multiple sports teams, was involved in the local indie games scene and helped organise the sci-fi society events.
Blog Highlights
Some posts related to my PhD work. Some are detailed posts to explain a problem to others, while others are slightly larger notes highlighting interesting ideas and properties related to approximation and optimisation.
Github Projects
I have a number of projects that are public, they are mostly just experiments and collaborating with others.
RadeonRays_SDK
This project was part of the Radeon Rays project which I worked on with the Radeon Technology teams at AMD.
Confetti
Confetti is an experiment I made to test simulating delay-line memory through the cables of the internet. It worked pretty nicely when we could get long enough chains of connections to maintain data within the wires long-enough!
ModernCPP_Examples
This project was to put together a collection of the modern features of C++ into a Visual Studio project to share with my friends so I can easily point them at compilable reference. This hasn’t had much love recently as the examples on cppreference and others are far more detailed and often interactive now!
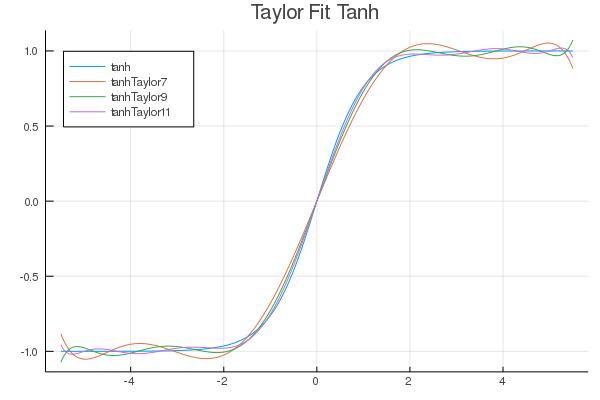
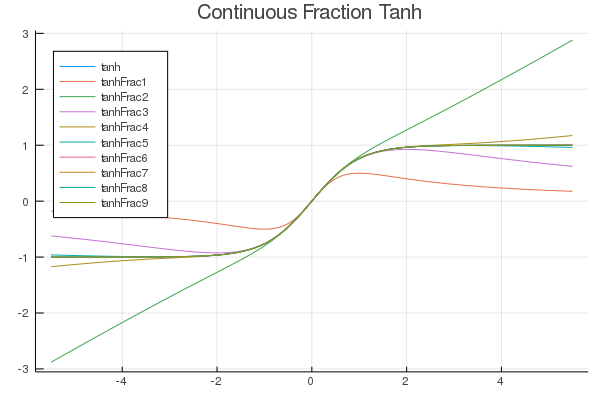
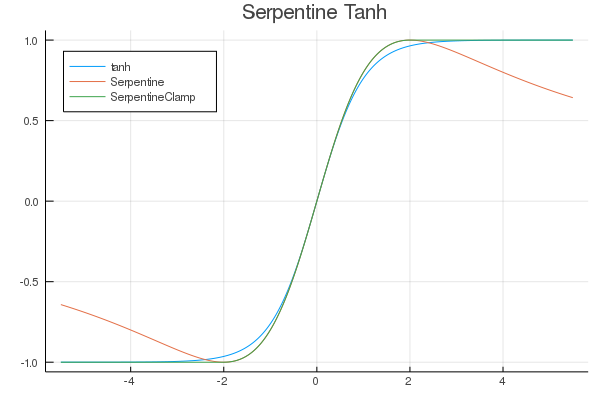
FastActivations.jl
A project which works with Flux.ml and my contributions there, to allow for custom faster activation functions in your neural networks.
| Fitted Functions | Continuous Fraction | Serpentine |
|---|---|---|
 |
 |
 |
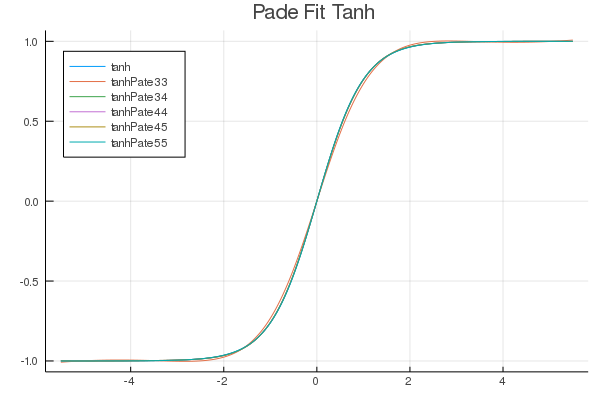 |
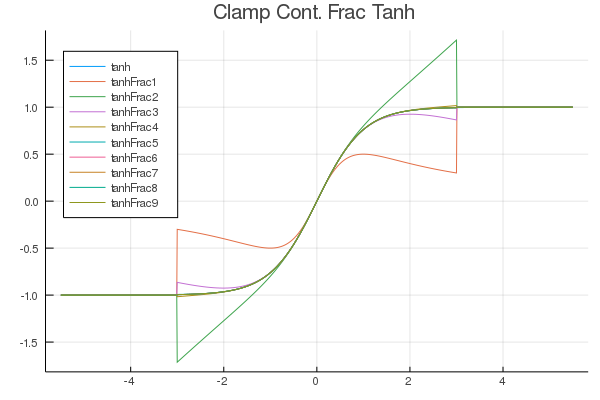 |
ApproximateComputations.jl
This is a small library which is used to perform automatic function approximation and replacement in Julia. It works well with ApproximationAnalysis.jl to provide bounded-error approximations.
XboxController.jl
Nice and simple small package for Julia to allow use of the Xbox controller. Makes exploring graphs in real-time at presentations much nicer!
Ditherings.jl and NormalMaps.jl
Extensions for Images.jl to provide simple image processing examples. Written to help me learn how Images.jl works.
Example of Dithering:
| Input | One-Bit | One-Bit RGB |
|---|---|---|
 |
 |
 |
Example of Normal generation:
| Input | Output |
|---|---|
 |
 |
| Base | Overlay | Result |
|---|---|---|
 |
 |
 |
Julia_Chip8_Emulator
An implementation of the CHIP-8 processor in Julia. Just a little project as I learned to write emulators.