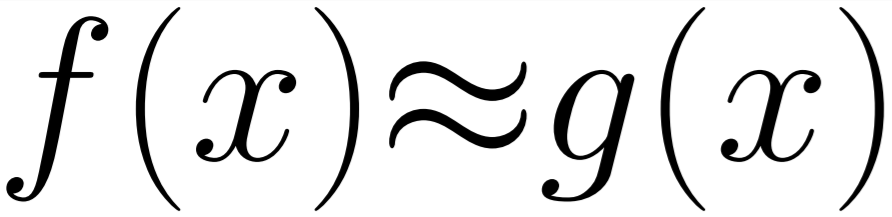In the last post we showed that small error in the activation function used for a network did not negatively impact the performance or output of a neural network (using our relatively small networks).
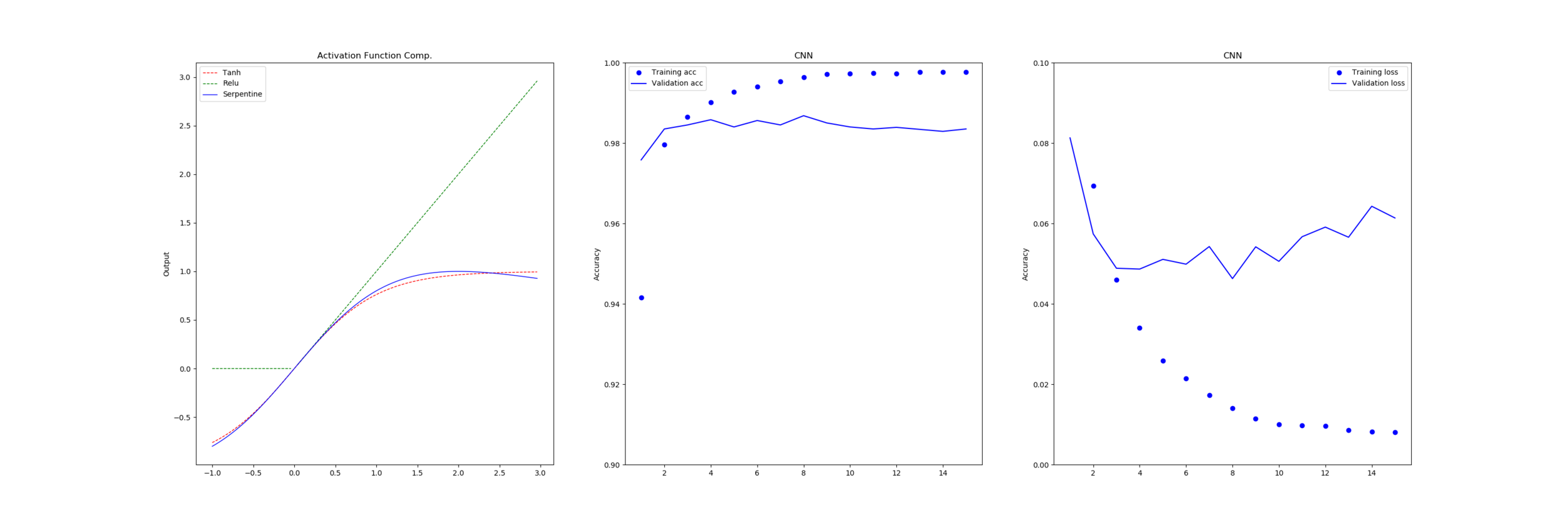
As part of our work on systems which are error tolerant, we took the different activation functions that are commonly used and an approximation known as the “serpentine” curve and ran it through our networks to see how they performed to determine if error in the activation function or the shape of the function had much of an impact.
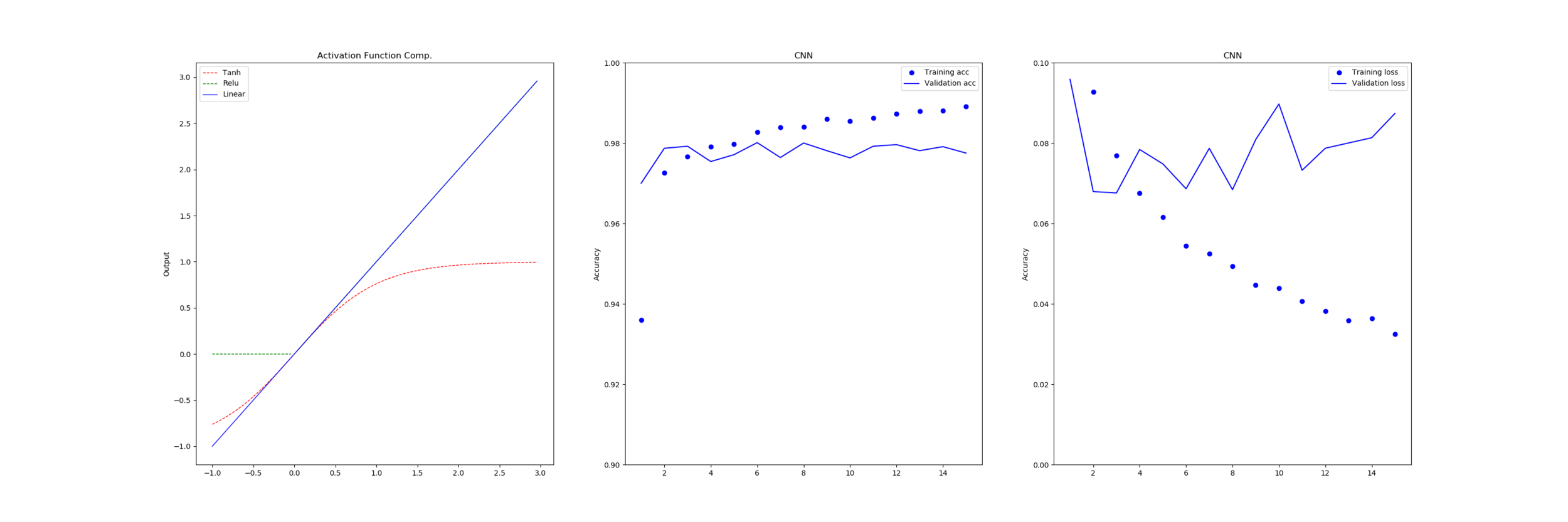
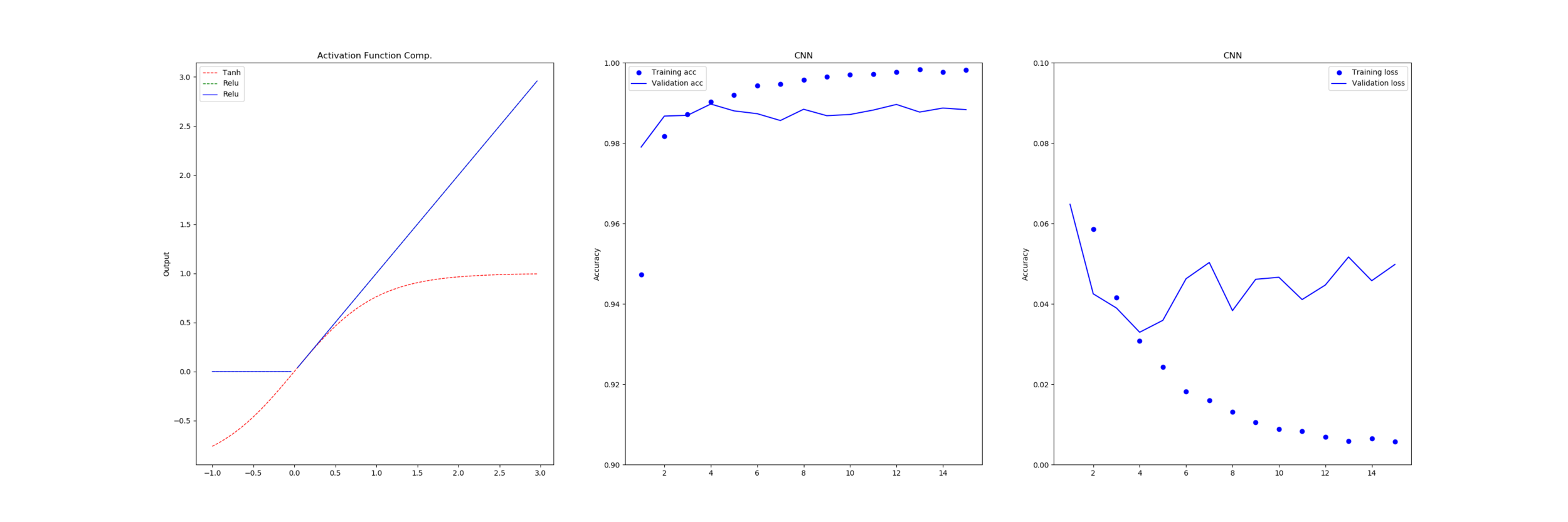
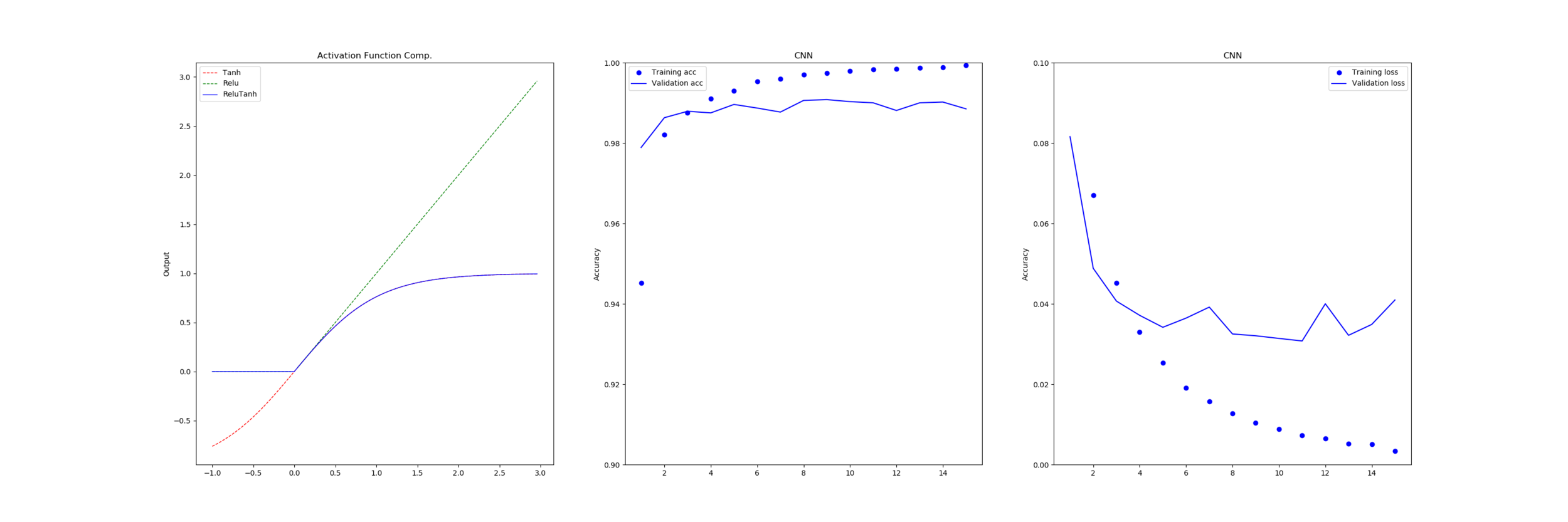
Below we show the series of results for each function with a 16-bit implementation and after that there is a table showing the amount of error relative to a full-precision for each.
The error is calculated by taking every half-precision floating point value between 0.0 and 5 and passing it into the target function and measuring the different from the full 64-bit implementation, as opposed to the earlier work where we compared approximations to their source.
From this we can see that dropping to 16-bit floating point doesn’t incur any penalty to the functions with only linear component (Relu, LinearX, Constant) as these functions all take an input that exists in half-precision and return the same input or a fixed output that is also a valid half-precision number without any chance of overflow or rounding.
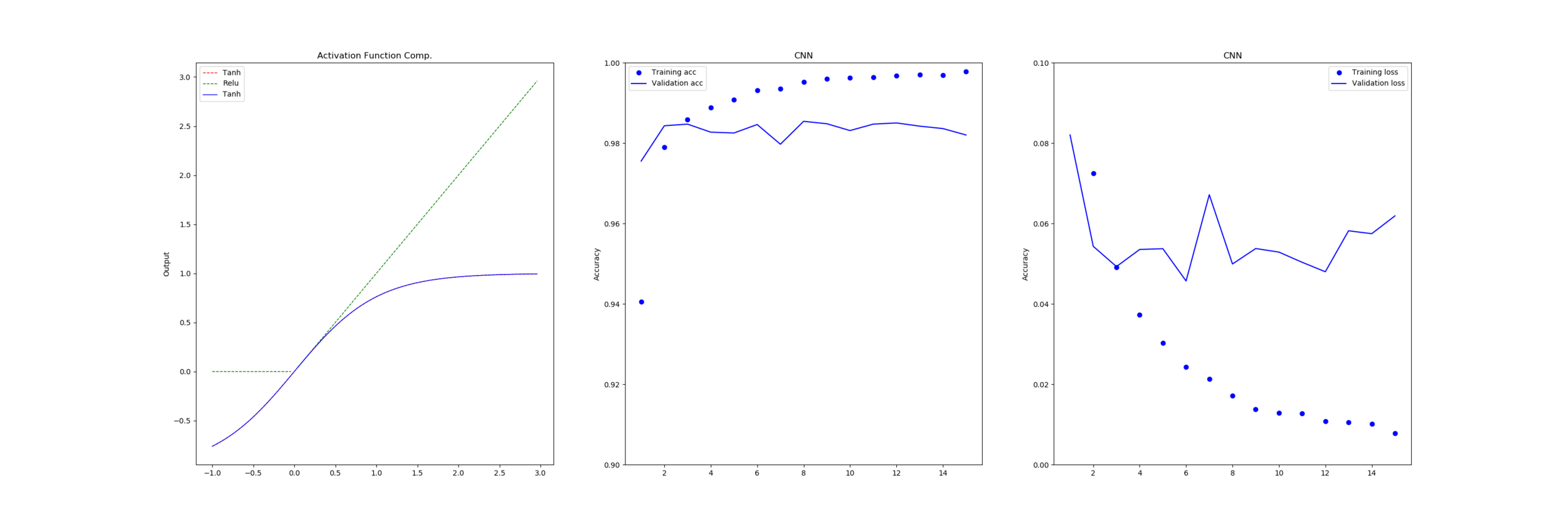
On the other hand our ‘tanh’ and ‘serpentine’ functions both perform calculations in half-float leading to errors which propagate to the return value. We can see by the median value that most results do no incur very much error at all but some values are very wrong.
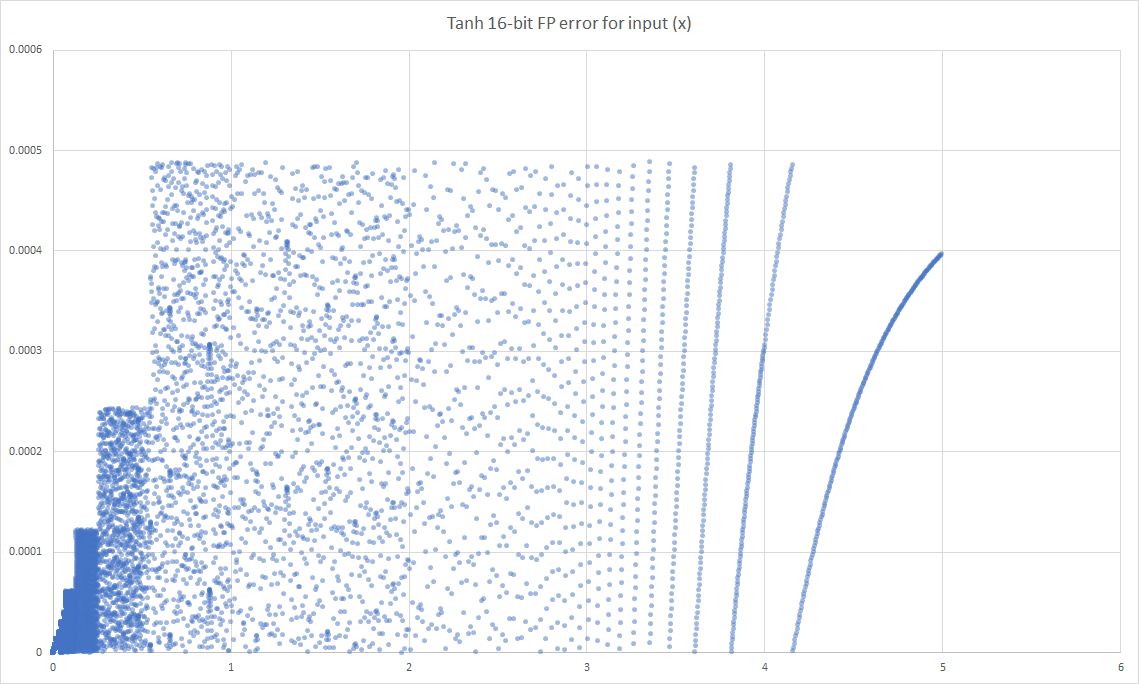
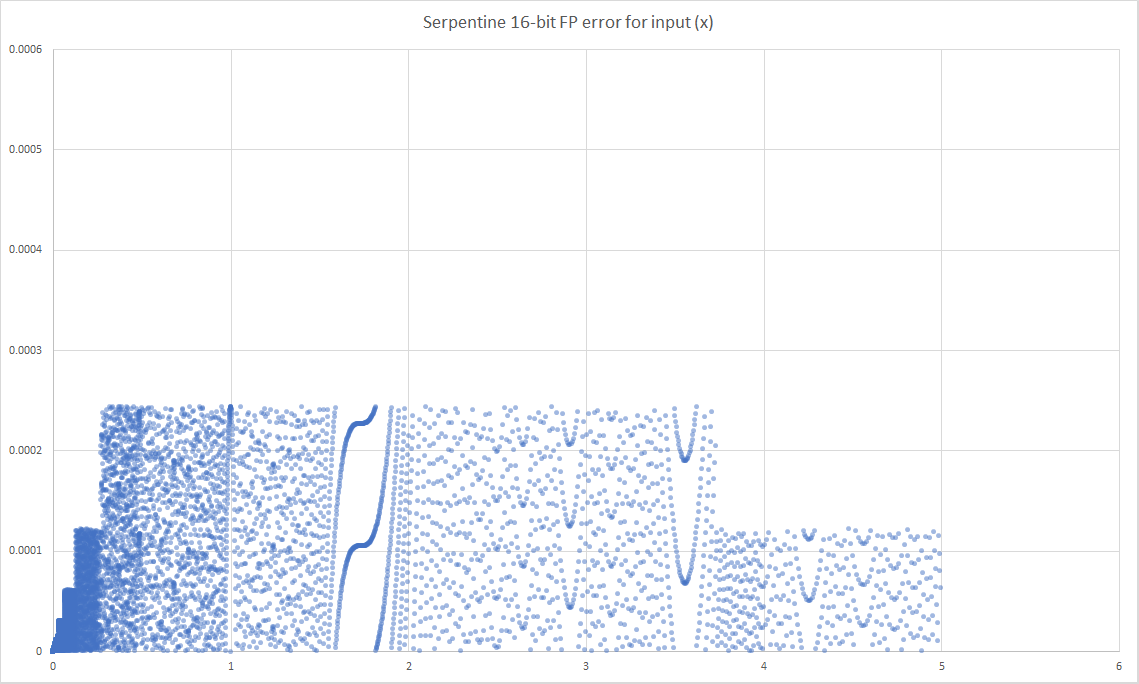
Noticeably the approximation of the ‘Tanh’ function, ‘Serpentine’, has lower maximum and average error. To inspect this further we plotted the error for every input in the range 0.0 to 5.0 for both functions.
In both results the inherent pattern of the floating-point numbers is visible, but much noticeable on the ‘serpentine’ plot. The exact pattern is a little worrying as it changes the pattern from being close enough to ‘random’ to possibly having some implication in error propagation.
In our tests the network we used appears to be tolerant enough of either error and give good enough results for both - however the sigmoid-like ‘serpentine’ function is much cheaper than the ‘tanh’ which raises the question why it isn’t being used instead.
Additionally, the error across the range is non-linear for both. If we were to use this in a network the weights which allow for input closer to 0 will have a more diverse set of choices for values and allowing for a higher-precision fit than those with much larger activation values. This should result in a change in how the network converges on the correct answer.
More importantly is the propagation of error. In neural networks there is the problem of exploding and diminishing gradients which is commonly known (and one of the reasons for the popularity of non-linear but basically linear functions like ReLu). Allowing error to propogate through an application means that the combined error could cause unwanted behaviour such as that with gradients but also that the gradient you are using during back propagation may not be correct for the activation function that is being used.
This leaves us with the question of how tolerant are networks to small errors in the activation function, particularly with low precision data-types. Are there certain patterns of input or weights which in conjunction with non-linear error would slow or distort the learning process? Or will this type of error on larger networks limit the convergence onto the best possible solution?