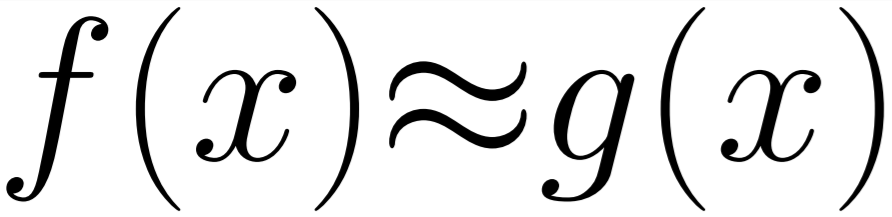We have put a few posts up now showing different techniques and thoughts on how to implement some kind of approximation to improve performance in your applications. What we hadn't covered was identifying what properties of the program are needed so that it can be approximated and how we can approach that process from a high level.
What is required of the program?
To approach the 'what' question we can start by classifying functions and algorithms into different types to understand how we can approach them:
No Golden Answers
This is probably the most obvious condition that has to be met for a program to be approached with approximation methods. The answer that the program returns has to be allowed to not be a specific perfect answer.Resilient Results
When we call a program resilient we mean that the returned result can be off by some margin and that result will be gracefully accepted and be acceptable. An example of this would be sensors returning information on a mobile device. The sensor data is often noisy or slightly unreliable so the mobile device correctly handles the information and removes anomalous results and still lands on or near enough to the correct conclusion. The same can be said for image encoding which takes correct information and returns an image which is not correct but is close enough to be accepted by the user as correct as it should be within the acceptable bounds of their vision.
JPEG compression
JPEG compression is a good example of this. Wikipedia has a good example of this (shown left) where the quality of the image decreases from right to left and we can see that for significant portion of that quality loss the image is acceptably clear.
Stochastic Results
If you are familiar with "real-time" raytracing you will have encountered these types of approximation frequently. Approaches such as Monte-Carlo algorithms and similar stochastic techniques. These programs can return a random selection of the answer that is statistically correct but cannot be predicted. This is useful when we want to sample parts of a final answer where calculating the total final answer would be too costly.
The video above shows a project I was involved in which uses stochastic methods to approximate lightmaps which converge on being the correct result over time.
If a program is able to correct over-time like this then it is possible to approximate a final answer before the work is fully complete, possibly within the bounds of acceptable error.
Self-correcting Program
A program that can self-correct from an erroneous input is definitely able to be exploited with approximation, when the cost of that correction is low. In the post that detailed approximation memoisation we gave the example of a path finding algorithm that gave near-enough results. That was acceptable because the user of the near-enough results was able to correct for the slight offset. Other examples of self-correcting programs include online multi-player games which use prediction to reduce the amount of network traffic required for each player in the game at all times. This type of prediction works because the small amount of error from where the game thinks the player is and where the player ends up being is compensated for, hopefully subtly and without impacting gameplay. This isn't always the case, some games allow for too much prediction and you see visible rubber banding - this is where the approximation is not able to correct for the lack of information accurately.Fail Rare/Fail Small
This type of scenario was covered in the article about approximation with multi-threading. When part of an application is allowed to fail but the program is able to compensate and continue anyway then it is open to be exploited for performance gains. This can take many forms as long as the error is handled correctly. Mobile phones can particularly exploit this by sleeping or slowing some features when it thinks the user isn't interested in the results. It is also applied in some network architectures.
How can we approach approximation?
For the second criteria we need to define different types of approximation at a high-level
Operation Level Approximation
We are able to change how our data interacts at a low level, for example we can change "a+a+a" to "3*a" - in floating-point these two examples are different despite being mathematically identical. So this is translation is technically an approximation because we have made the result different than the programmers intent (to our knowledge). Normally a compiler wont make this change for that reason, but if we relax that rule we can do operation level transformations like this to try and find optimisations at this level. This can be taken to more extreme examples by being more loose, such as saying we only care about accuracy +/- 0.1, so any number that is passed to an addition that is less than that we throw away and don't do the addition.Data-type Level Approximation - This is the most commonly found approximation in regular programming. We can change how we represent data in the code, with more or less precision this is normally done through standard types (float, double, long double... etc) but could also be expressed through custom software types with their own interesting behaviours.
Algorithm Level Approximation - These is the most common approach for the types of programs that are open to optimisation that we listed above. This type of optimisation can be almost anything such as: loop perforation, step skipping, probabilistic algorithms, limited search, aggressive early-out optimisation. Really whatever you can think of that will cause the results to be returned in an approximated manner.
That pretty much covers the basics of when and how to approach optimisation in a modern code project - but dont forget some of the old techniques are still around and doing great too. It could be argued that many search and learning algorithms that are not able to be applied with a robust and provable mathematical model are simply approximating the result as best they can.