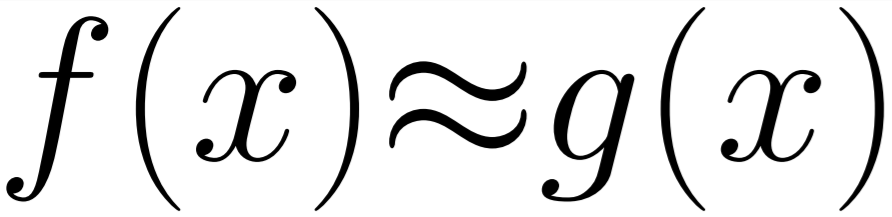Many programmers writing software today are unaware of the precision with which they are currently writing applications. A general rule of convenience, there not being any errors and no large performance impact dictate many choices in the types and algorithms being used to get the results desired.

Quite often it is seen that a programmer will use an 'int' array to store numbers only ranging from zero to four. In this situation the programmer has given far too much precision in the type and is losing memory performance by having to load all the extra bit representing numbers above four. Additionally a programmer may use a math function such as 'std::sinf' to calculate some value of sin for an input but they are only interested in the result of sin to three decimal places - in which case 'std::sinf' is doing far more work that is necessary and working at a much higher precision to conform to the C Math Specification.

The need to run at a lower precision can come from all sorts of requirements. From the need to fit the calculation within a set number or cycles or simply to reduce the power consumption of the device. Many of the techniques employed in functions to get lower precision or estimated results are referenced under the category of Approximate Computation.

In the case of types, most modern programming languages do not provide a type system which allows a clear selection of the precision for most basic types. The options are often quantised to 8/16/32/64/128-bit representations to make an easier match to the common hardware available. This is known as Software-Hardware Co-design.

However, in the case of functions we are given the full control to calculate the precision to what we need and then store into one of the predefined types. There are all sorts of numerical techniques for calculating the result of different mathematical functions to different precision and some of these can be seen in the differences between math libraries which do not conform to the C Math Specification.

We can conclude that we are, for practical reasons, stuck with standard types but can allow any function to work a given precision. How would we go about it if we wanted to implement our own approximate 'std::sinf' function for a small section of a large codebase already using the standard library implementation?
We could do that quite simply by adding our new function like any other - but what if we wanted to pass a 'float' to that function? We would need to create our own namespace, or rename the function - this would mean significant rewrites to the code base.
And we would want to make the use of this approximate variation safe - the result of a lower precision sin mixed with the real precision sin could cause some trouble as any trigonometric identities would also be approximate. Basically, we want to ensure we don't mix an approximate result with a precise one without the programmer explicitly stating to do so.

To meet the requirements above we can use a wrapper type around basic types with a templated precision flag. This type can then be used for overloading the call to 'sinf' - so that no function calls need to change and through the type system a 'float' could not be used with an 'ApproxType<float>' without the programmer explicitly requesting the base 'float' type from the wrapper. This means the programmer would have to change the types of the objects in the code base that are going to be less accurate but none of the functional logic. Additionally, it allows for the user to specify a maximum level of error that this type accepts, by allowing this we can statically switch calls made with the approximate type to the function which provides the requested level of precision.

For example, a float which says it accepts 10% error in its result that is passed to 'sinf' will be forwarded to an implementation of 'sinf' that at minimum meets that requirement.

So, with those rules and a plan - this is how to implement such a design in C++!

We want to start with the Approximate Wrapper Type. This is our class which will essentially be the type of the object that is normally passed to the function but is marked up statically with the level of accuracy desired. It is also given a 'Get' function to allow the data to be removed from the object. This is the method by which the programmer is expressing that the accuracy is final and safe to use outside of the type-safety. Ideally, we would want to also have the type specify minimum and maximum values and include all the copy rules to allow that to work - but for this basic implementation this will do to show the concept.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16template< typename T, int accNumurator >
class ApproxType
{
public:
	ApproxType(T _in)
	{
		m_data = _in;
	}

	T& Get()
	{
		return m_data;
	}

	T	m_data;
};

In this example I am using a Taylor Approximation of Sin generated through my build system. It looks a bit scary but is just a simple polynomial.

1
2
3
4
5
6
7constexpr float ApproxSin_Order7(const float _x) noexcept
{
	return ((-0.00001633129816711214847969706187580f*(1.0f)) + (1.00037993800406788125201273942366242f*(_x)) 
			+ (-0.00211754585380569430516639606310036f*(_x* _x)) + (-0.16175605700248782414796266948542325f*(_x* _x * _x)) 
			+ (-0.00577124859440479066885476555626155f*(_x* _x * _x * _x)) + (0.01203154857279084034848981588083916f*(_x* _x * _x * _x * _x)) 
			+ (-0.00127402703149161102696984571025496f*(_x* _x * _x * _x * _x * _x)) + (-0.00000043655425207306325578100769137f*(_x* _x * _x * _x * _x * _x * _x)));
}

Now we want to Overload 'sinf' with our function which takes our wrapped approximate type. In this function we are specifying how accurate our approximate implementation is (accuracy = 8) and using an 'std::conditional' to select which function should be called. In this case, if the approximate type that is passed in allows this level or accuracy then it will call the Taylor Approximation of Sin other wise it will simply call 'std::sinf'.

This logic is all performed with constexpr and static types where possible so that this code can be evaluated at compile time to reduce this down to as close as possible to a single function call.

1
2
3
4
5
6
7
8template< typename T, int accNumurator >
float sinf(ApproxType<T, accNumurator> _x)
{
	static constexpr int accuracy = 8;
	typedef std::conditional < accuracy >= accNumurator, FuncWrapper<ApproxSin_Order7>, FuncWrapper<std::sinf> >::type A;

	return A::Call(_x.Get());
}

You may have noticed in the above example that the 'std::conditional' doesn't actually contain function pointers but function pointers wrapped in a class called FuncWrapper. This is because std::conditional only takes types but we want to be able to do a compile-time selection. So we wrap the function pointer is a class which has a static function call to run the wrapped function. The call to 'std::conditional' gives us the correct type to then call the function on. It is a little bit of a hack, but is what has to be done for now until C++ gets good support for a Static If.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10template< float func(float) >
class FuncWrapper
{
public:

	static float Call(float _in)
	{
		return func(_in);
	}
};

If we put this all together we can see how the code is used. We havent had to make any special calls to the function we replaced as it is all handled by the overloading of the function. The compiler has then generated the correct function calls for each based on the level of accuracy we allow for each of the ApproxType's.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12int main()
{
	float var = 0.5f;
	ApproxType<float, 6> approx(var);
	ApproxType<float, 9> approxhigh(var);
	
	float approxreslow  = sinf(approx);		// Calls the approximate function
	float approxreshigh = sinf(approxhigh); // Calls std::sinf from the Approximate Wrapper
	float accurateres	= sinf(var);		// Calls std::sinf

	return 0;
}

These functions can now be dropped into a codebase and then through specifying where you want the types to be approximate, we can access all the possibilities of Approximate Computing with very minimal changes.

Thanks for reading. All the code in one place:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59#include <cmath>

template< typename T, int accNumurator >
class ApproxType
{
public:
	ApproxType(T _in)
	{
		m_data = _in;
	}

	T& Get()
	{
		return m_data;
	}

	T	m_data;
};

template< float func(float) >
class FuncWrapper
{
public:

	static float Call(float _in)
	{
		return func(_in);
	}
};

constexpr float ApproxSin_Order7(const float _x) noexcept
{
	return ((-0.00001633129816711214847969706187580f*(1.0f)) + (1.00037993800406788125201273942366242f*(_x)) 
			+ (-0.00211754585380569430516639606310036f*(_x* _x)) + (-0.16175605700248782414796266948542325f*(_x* _x * _x)) 
			+ (-0.00577124859440479066885476555626155f*(_x* _x * _x * _x)) + (0.01203154857279084034848981588083916f*(_x* _x * _x * _x * _x)) 
			+ (-0.00127402703149161102696984571025496f*(_x* _x * _x * _x * _x * _x)) + (-0.00000043655425207306325578100769137f*(_x* _x * _x * _x * _x * _x * _x)));
}

template< typename T, int accNumurator >
float sinf(ApproxType<T, accNumurator> _x)
{
	static constexpr int accuracy = 8;
	typedef std::conditional < accuracy >= accNumurator, FuncWrapper<ApproxSin_Order7>, FuncWrapper<std::sinf> >::type A;

	return A::Call(_x.Get());
}

int main()
{
	float var = 0.5f;
	ApproxType<float, 6> approx(var);
	ApproxType<float, 9> approxhigh(var);
	
	float approxreslow  = sinf(approx);		// Calls the approximate function
	float approxreshigh = sinf(approxhigh); // Calls std::sinf from the Approximate Wrapper
	float accurateres	= sinf(var);		// Calls std::sinf

	return 0;
}