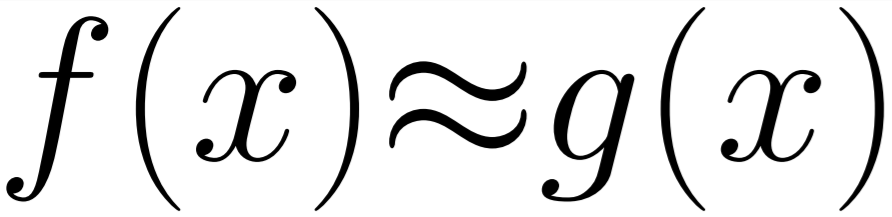When dealing with error we not only need to know how to measure it, but also how what the error of a value that is produced by performing an operation on two values with differing levels of error.
For example, if we have a variable A which has an error of +/- 5 and a variable B which has an error of +/- 3, how would we calculate the accuracy of the result of A+B?
It turns out this can be solved by the 'Rules for Error Propagation'. These rules define how the combination of values of different uncertainty interact to produce a new value of uncertainty.
The main 'Rules of Error Propagation'.
The equations we are given to calculate the solution to our problem is quite simple. We simply place our values of δA (+/- 5) and δB (+/- 3) into the first equation (as we are doing addition, 'A + B').
This results in our new value having a potential error of 5.83 which as we expected is greater than either of the inputs as error in this situations can only grow due to missing information.
So we can see that with this method of approaching error it is relatively simple to encode this into your software to analyse values as they are passed through functions.