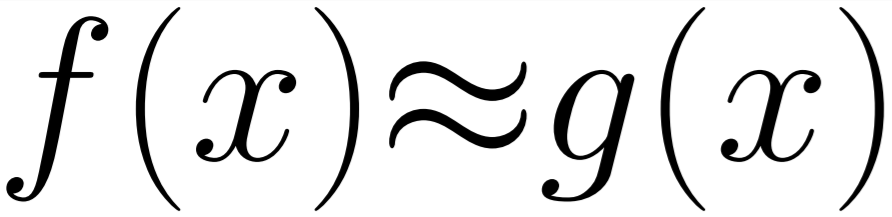The first in our guide to error and approximation in computing is starting with absolute and relative error.

Error in measurement or a calculation can be easily thought of as a simple thing, but when we are trying to be precise in our description of error and how it effects the validity of our results we need to consider the context of the error that we are talking about. To do this we need to define the error.

Starting with Absolute Error. Absolute error is the total error. For most tools we use in the real-world to measure things they are often marked with +/- 1mm or similar to tell the user the absolute amount of error in measurement. In computing terms, we could say the absolute error in a floating point value that we have just assigned a real number is the maximum amount of rounding possible for a real number in that range. Quite simple and easy to understand.

Expanding on that we also have the Mean Absolute Error, as it may sound this is a quite straight forward extension of the absolute error. This is simply the average (mean) of the errors between related results in a series. So the average value of f(x) - g(x) for all x in a series where f is the correct function and g is some approximation. This is used when evaluating error on continuous data as opposed to single measurement results.

Finally we have Relative Error, this is calculated from the Absolute Error and the total range you are working with. It gives you the error in your measurement relative to the total outcome. For example, if we are measuring weight and our scales are accurate to +-1Kg and the thing we are weighing is 20kg then we have a Relative Error of 5%. But if we were weighing something that was 2000kg then the error is 0.05% which is much better. This is an important consideration when measuring error in software as it can directly link the precision of the data type you are using to the size of the data you are trying to store.

That's about it on Absolute and Relative error. All quite simple but important to know the difference when reading or writing a paper so that you understand the context the error is being described in.